Advancing the LFSR

LFSR logic is commonly used in hardware and software to generate pseudo-random data. An n-bit LFSR cycles between as many as 2^n - 1 unique, non-zero states.

In some contexts, the output of the LFSR is considered a single bit, the state of the right-most register in these examples. In other situations, the output is the state of all of the registers.

Two configurations are possible: Galois (also known as type 2), and Fibonacci (also known as type 1). The single bit output at the right-most register is identical for both configurations. The output at the other bit positions differ, but only by a time delay. The time delay for each bit position can be found by inspection for the Fibonacci configuration, and with a calculation for the Galois configuration, as shown below.

Both Galois and Fibonacci configurations can be drawn with left shifting registers or right shifting registers. But the choice of shift direction is not important. Because no inherently directional operation such as carry propagation is involved, the operation of the two mirror each other. The shift direction used here has been chosen to accommodate comparing the Galois and Fibonacci configurations.

Galois configuration for polynomial x^7 + x^6 + x^3 + x + 1

The state of the LFSR at time t can be written in terms of the previous state. The equations are found by inspection of the circuit:

 g0 (t) = g6 (t-1)             (1)
 g1 (t) = g0 (t-1) ^ g6 (t-1) 
 g2 (t) = g1 (t-1)            
 g3 (t) = g2 (t-1) ^ g6 (t-1) 
 g4 (t) = g3 (t-1)            
 g5 (t) = g4 (t-1)            
 g6 (t) = g5 (t-1) ^ g6 (t-1)

In matrix form, the current state is multiplied by the matrix to give the next state. Each bit in the current state selects a row in the matrix. The selected rows are exclusive ored together to produce the next state.

  0000010
  0000100
  0001000
  0010000
  0100000
  1000000
  1001011
 

Fibonacci configuration for polynomial x^7 + x^6 + x^3 + x + 1

The state of the LFSR at time t can be written in terms of the previous state. The equations are found by inspection of the circuit:

 f0 (t) = f1 (t-1)                                   (2)
 f1 (t) = f2 (t-1)                                  
 f2 (t) = f3 (t-1)                                  
 f3 (t) = f4 (t-1)                                  
 f4 (t) = f5 (t-1)                                  
 f5 (t) = f6 (t-1)                                  
 f6 (t) = f0 (t-1) ^ f1 (t-1) ^ f3 (t-1) ^ f6 (t-1)

The next state matrix for the Fibonacci configuration:

  1000000
  1000001
  0000010
  1000100
  0001000
  0010000
  1100000

The next state matrix of one LFSR configuration is the transpose of the next state matrix of the other configuration.

The LFSRs cycle through the following states when the registers are initially loaded with 0000001:

      Galois       Fibonacci
t     g6···g0      f6···f0
0     0000001      0000001
1     0000010      1000000
2     0000100      1100000
3     0001000      1110000
4     0010000      1111000
5     0100000      0111100
6     1000000      1011110
7     1001011      1101111
8     1011101      0110111
9     1110001      0011011
10    0101001      1001101
11    1010010      1100110
12    1101111      0110011
13    0010101      0011001
14    0101010      0001100
15    1010100      1000110
16    1100011      0100011
17    0001101      0010001
18    0011010      1001000
19    0110100      0100100
20    1101000      0010010
21    0011011      1001001
22    0110110      1100100
23    1101100      1110010
24    0010011      0111001
25    0100110      0011100
26    1001100      1001110
27    1010011      1100111
28    1101101      1110011
29    0010001      1111001
30    0100010      1111100
31    1000100      0111110
32    1000011      0011111
33    1001101      1001111
34    1010001      0100111
35    1101001      0010011
36    0011001      0001001
37    0110010      0000100
38    1100100      0000010
39    0000011      1000001
40    0000110      0100000
41    0001100      0010000
42    0011000      0001000
43    0110000      1000100
44    1100000      1100010
45    0001011      0110001
46    0010110      1011000
47    0101100      0101100
48    1011000      1010110
49    1111011      0101011
50    0111101      1010101
51    1111010      0101010
52    0111111      0010101
53    1111110      1001010
54    0110111      1100101
55    1101110      0110010
56    0010111      1011001
57    0101110      1101100
58    1011100      0110110
59    1110011      1011011
60    0101101      0101101
61    1011010      0010110
62    1111111      1001011
63    0110101      0100101
64    1101010      1010010
65    0011111      0101001
66    0111110      0010100
67    1111100      0001010
68    0110011      0000101
69    1100110      1000010
70    0000111      0100001
71    0001110      1010000
72    0011100      1101000
73    0111000      0110100
74    1110000      0011010
75    0101011      0001101
76    1010110      0000110
77    1100111      1000011
78    0000101      1100001
79    0001010      0110000
80    0010100      0011000
81    0101000      1001100
82    1010000      0100110
83    1101011      1010011
84    0011101      1101001
85    0111010      1110100
86    1110100      1111010
87    0100011      1111101
88    1000110      1111110
89    1000111      1111111
90    1000101      0111111
91    1000001      1011111
92    1001001      0101111
93    1011001      1010111
94    1111001      1101011
95    0111001      0110101
96    1110010      1011010
97    0101111      1101101
98    1011110      1110110
99    1110111      0111011
100   0100101      1011101
101   1001010      1101110
102   1011111      1110111
103   1110101      1111011
104   0100001      0111101
105   1000010      0011110
106   1001111      0001111
107   1010101      1000111
108   1100001      1100011
109   0001001      1110001
110   0010010      0111000
111   0100100      1011100
112   1001000      0101110
113   1011011      0010111
114   1111101      0001011
115   0110001      1000101
116   1100010      0100010
117   0001111      1010001
118   0011110      0101000
119   0111100      1010100
120   1111000      1101010
121   0111011      1110101
122   1110110      0111010
123   0100111      0011101
124   1001110      0001110
125   1010111      0000111
126   1100101      0000011
<cycle repeats starting here>

Equivalence of Galois and Fibonacci configurations for polynomial x^7 + x^6 + x^3 + x + 1

Notice that the output, when taken as the single right-most register, is the same for both configurations. This is true in general, and can be demonstrated by writing the output equations for the right-most register of both configurations in terms of previous values of the register. For the Fibonacci configuration, start with equations (2) and solve for f0 (t) as a function of f0 at times t-1 through t-7:

f0 (t) = f1 (t-1)
f0 (t) = f2 (t-2)
f0 (t) = f3 (t-3)
f0 (t) = f4 (t-4)
f0 (t) = f5 (t-5)
f0 (t) = f6 (t-6)
f0 (t) = f0 (t-7) ^ f1 (t-7) ^ f3 (t-7) ^ f6 (t-7)
f0 (t) = f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)

f1 (t) = f0 (t+1)
       = f0 (t-6) ^ f0 (t-5) ^ f0 (t-3) ^ f0 (t-0)
       = f0 (t-6) ^ f0 (t-5) ^ f0 (t-3) ^ f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-5) ^ f0 (t-3) ^ f0 (t-7) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-7) ^ f0 (t-5) ^ f0 (t-4) ^ f0 (t-3) ^ f0 (t-1)

f2 (t) = f1 (t+1)
       = f0 (t-6) ^ f0 (t-4) ^ f0 (t-3) ^ f0 (t-2) ^ f0 (t-0)
       = f0 (t-6) ^ f0 (t-4) ^ f0 (t-3) ^ f0 (t-2) ^ f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-3) ^ f0 (t-2) ^ f0 (t-7) ^ f0 (t-1)
       = f0 (t-7) ^ f0 (t-3) ^ f0 (t-2) ^ f0 (t-1)

f3 (t) = f2 (t+1)
       = f0 (t-6) ^ f0 (t-2) ^ f0 (t-1) ^ f0 (t-0)
       = f0 (t-6) ^ f0 (t-2) ^ f0 (t-1) ^ f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-7) ^ f0 (t-4) ^ f0 (t-2)

f4 (t) = f3 (t+1)
       = f0 (t-6) ^ f0 (t-3) ^ f0 (t-1)

f5 (t) = f4 (t+1)
       = f0 (t-5) ^ f0 (t-2) ^ f0 (t-0)
       = f0 (t-5) ^ f0 (t-2) ^ f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-5) ^ f0 (t-2) ^ f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-7) ^ f0 (t-6) ^ f0 (t-5) ^ f0 (t-4) ^ f0 (t-2) ^ f0 (t-1)

f6 (t) = f5 (t+1)
       = f0 (t-6) ^ f0 (t-5) ^ f0 (t-4) ^ f0 (t-3) ^ f0 (t-1) ^ f0 (t-0)
       = f0 (t-6) ^ f0 (t-5) ^ f0 (t-4) ^ f0 (t-3) ^ f0 (t-1) ^ f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)
       = f0 (t-5) ^ f0 (t-3) ^ f0 (t-7)
       = f0 (t-7) ^ f0 (t-5) ^ f0 (t-3)

 f0 (t) = f0 (t-7) ^ f0 (t-6) ^ f0 (t-4) ^ f0 (t-1)                        (3)
 f1 (t) = f0 (t-7) ^ f0 (t-5) ^ f0 (t-4) ^ f0 (t-3) ^ f0 (t-1)            
 f2 (t) = f0 (t-7) ^ f0 (t-3) ^ f0 (t-2) ^ f0 (t-1)                       
 f3 (t) = f0 (t-7) ^ f0 (t-4) ^ f0 (t-2)                                  
 f4 (t) = f0 (t-6) ^ f0 (t-3) ^ f0 (t-1)                                  
 f5 (t) = f0 (t-7) ^ f0 (t-6) ^ f0 (t-5) ^ f0 (t-4) ^ f0 (t-2) ^ f0 (t-1) 
 f6 (t) = f0 (t-7) ^ f0 (t-5) ^ f0 (t-3)

The coefficients for the terms in the above equations can also be found with a calculation:

    t-1·t-7        calculation    p7····p0 p6···p0
f0  1001011        gf2util modmul,11001011,1001011,1
f1  1011101        gf2util modmul,11001011,1001011,10
f2  1110001        gf2util modmul,11001011,1001011,100
f3  0101001        gf2util modmul,11001011,1001011,1000
f4  1010010        gf2util modmul,11001011,1001011,10000
f5  1101111        gf2util modmul,11001011,1001011,100000
f6  0010101        gf2util modmul,11001011,1001011,1000000

   

For the Galois configuration, start with equations (1) and solve for g0 (t) as a function of g0 at times t-1 through t-7:
g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g6 (t-1)
g2 (t) = g1 (t-1)
g3 (t) = g2 (t-1) ^ g6 (t-1)
g4 (t) = g3 (t-1)
g5 (t) = g4 (t-1)
g6 (t) = g5 (t-1) ^ g6 (t-1)

g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g1 (t-1)
g3 (t) = g2 (t-1) ^ g0 (t)
g4 (t) = g3 (t-1)
g5 (t) = g4 (t-1)
g6 (t) = g5 (t-1) ^ g0 (t)

g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g2 (t-1) ^ g0 (t)
g4 (t) = g3 (t-1)
g5 (t) = g4 (t-1)
g6 (t) = g5 (t-1) ^ g0 (t)

g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-3) ^ g0 (t-2) ^ g0 (t)
g4 (t) = g3 (t-1)
g5 (t) = g4 (t-1)
g6 (t) = g5 (t-1) ^ g0 (t)

g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-3) ^ g0 (t-2) ^ g0 (t)
g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
g5 (t) = g4 (t-1)
g6 (t) = g5 (t-1) ^ g0 (t)

g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-3) ^ g0 (t-2) ^ g0 (t)
g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)
g6 (t) = g5 (t-1) ^ g0 (t)

g0 (t) = g6 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-3) ^ g0 (t-2) ^ g0 (t)
g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)
g6 (t) = g0 (t-6) ^ g0 (t-5) ^ g0 (t-3) ^ g0 (t)

g0 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1)
g1 (t) = g0 (t-1) ^ g0 (t)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-3) ^ g0 (t-2) ^ g0 (t)
g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)
g6 (t) = g0 (t-6) ^ g0 (t-5) ^ g0 (t-3) ^ g0 (t)
g0 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1)
g1 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-2) ^ g0 (t-1)
g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)
g6 (t) = g0 (t-7) ^ g0 (t-5) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
 g0 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1)                        (4)
 g1 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4)                                  
 g2 (t) = g0 (t-2) ^ g0 (t-1)                                             
 g3 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-2) ^ g0 (t-1) 
 g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)                                  
 g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)                                  
 g6 (t) = g0 (t-7) ^ g0 (t-5) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)

The coefficients for the terms in the above equations can also be found with a calculation:

    t-1·t-7                      p7····p0 
g1  0001011       gf2util modmul,11001011,11000000,1
g2  1100000       gf2util modmul,11001011,01100000,1
g3  1111011       gf2util modmul,11001011,10110000,1
g4  1011000       gf2util modmul,11001011,01011000,1
g5  0101100       gf2util modmul,11001011,00101100,1
g6  1011101       gf2util modmul,11001011,10010110,1
g0  1001011       gf2util modmul,11001011,01001011,1

 

The above shows that for the LFSR using polynomial x^7 + x^6 +x^3 + x + 1, the output of the right-most register is the same for both the Galois and Fibonacci configurations.

 

Equivalence of Galois and Fibonacci configurations, general case

A generalization of the example above can be made that is valid for any polynomial. For a Fibonacci configuration with n registers,

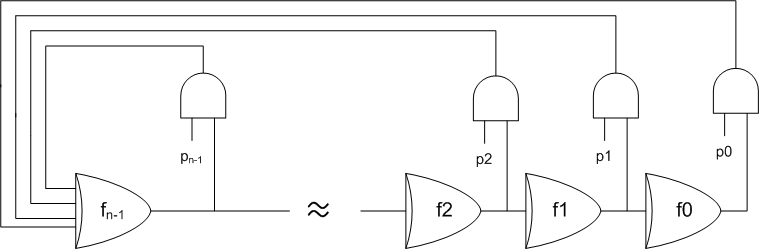
Let p0 through pn-1 be the n polynomial coefficients. The output of a register is an input to the exclusive-or gate if the corresponding polynomial coefficient is non-zero. Pn is assumed to be non-zero and does not correspond to a exclusive-or gate input.

f0 (t) = f1 (t-1)
f1 (t) = f2 (t-1)
f2 (t) = f3 (t-1)
    ···
fn-1 (t) = p0f0 (t-1) ^ p1f1 (t-1) ... ^ pn-1fn-2 (t-1)
 
f0 (t) = f1 (t-1)
f0 (t) = f2 (t-2)
f0 (t) = f3 (t-3)
    ···
f0 (t) = fn-1 (t-(n-1))

f0 (t) = p0f0 (t-n) ^ p1f1 (t-n) ^ p2f2 (t-n) ... ^ fn-1 (t-n)
f0 (t) = p0f0 (t-n) ^ p1f0 (t-(n-1)) ^ p2f0 (t-(n-2)) ... ^ pn-1f0 (t-1)
 
For a Galois configuration with n registers,
 
 
Let p0 through pn-1 be the n polynomial coefficients. The input of a register is exclusive-ored with the output of register gn-1 if the corresponding polynomial coefficient is non-zero. Pn is assumed to be non-zero and does not correspond to a exclusive-or gate input.

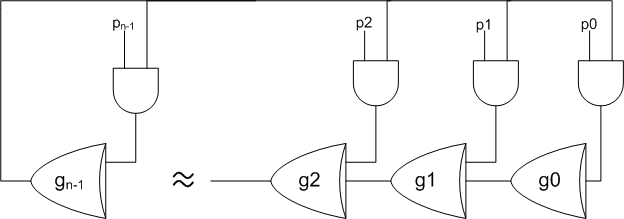
g0 (t) =            p0*gn-1 (t-1)
g1 (t) = g0 (t-1) ^ p1*gn-1 (t-1)
g2 (t) = g1 (t-1) ^ p2*gn-1 (t-1)
g3 (t) = g2 (t-1) ^ p3*gn-1 (t-1)
    ···
gn-1 (t) = gn-2 (t-1) ^ pn-1*gn-1 (t-1)

g1 (t) = g0 (t-1) ^ p1*g0 (t)
g2 (t) = g1 (t-1) ^ p2*g0 (t)
g3 (t) = g2 (t-1) ^ p3*g0 (t)
    ···
gn-1 (t) = gn-2 (t-1) ^ pn-1*g0 (t)

g1 (t) = g0 (t-1) ^ p1*g0 (t)
g2 (t) = g0 (t-2) ^ p1*g0 (t-1) ^ p2*g0 (t)

g1 (t) = g0 (t-1) ^ p1*g0 (t)
g2 (t) = g0 (t-2) ^ p1*g0 (t-1) ^ p2*g0 (t)
g3 (t) = g0 (t-3) ^ p1*g0 (t-2) ^ p2*g0 (t-1) ^ p3*g0 (t)
    ···
gn-1 (t) = g0 (t-(n-1)) ^ p1*g0 (t-(n-2)) ^ p2*g0 (t-(n-3)) ... ^ pn-1*g0 (t)
g0 (t) = g0 (t-n) ^ p1*g0 (t-(n-1)) ^ p2*g0 (t-(n-2)) ... ^ pn-1*g0 (t-1)
 

Advancing the LFSR
 
For the previous examples, all of the LFSR states can be found directly. But if the LFSR contains hundreds of registers, for example, there are too many states to compute directly. It is still possible to find an arbitrary state, however.
 
The approach described here is to recognize that the Galois LFSR configuration functions as a finite field multiplier. From the first example, the register bit values can represent polynomial coefficients. The primitive element that generates the field elements is the polynomial x^1, when implemented with an LFSR. The polynomial operations are done modulo x^7 + x^6 + x^3 + x + 1. Here is the first example output with the polynomial representation:
 
0   0000001 α^0 = x^0
1   0000010 α^1 = x^1
2   0000100 α^2 = x^2
    ···
124 1001110 α^124 = x^6 + x^3 + x^2 + x
125 1010111 α^125 = x^6 + x^4 + x^2 + x +1
126 1100101 α^126 = x^6 + x^5 + x^2 +1
 
Finite fields operations are well understood and described in many textbooks. A utility to do some basic operations, gf2util, is available in source form here, and win32 executable here. To make the utility generate the output above, use:
gf2util modpower,11001011,10,0
gf2util modpower,11001011,10,1
gf2util modpower,11001011,10,2
    ···
gf2util modpower,11001011,10,124
gf2util modpower,11001011,10,125
gf2util modpower,11001011,10,126
The utility uses the square and multiply method to do the exponentiation in a small number of steps.
 
The above procedure is practical for LFSRs that are too large to be advanced through every state, and will find any state in the sequence, assuming the sequence starts with 1. If the LFSR starting state is not 1, the effect of the starting state can be accounted for with an extra multiplication, because α^(b+c) = α^b * α^c. The case of starting state 1 becomes α^(b+0) = α^b * α^0 =  α^b. Just multiply, modulo the primitive polynomial, the result of advancing state 1, by the new starting value. For example, to advance the state 0101001 (t=10) by 50 steps, use gf2util modpower,11001011,10,50 to get α^50=0111101. Then use gf2util modmul,11001011,0111101,0101001 to get 0101101.
 
The method above handles finding a Galois LFSR ending state after initial state is clocked a certain number of times. But what about doing the same for the Fibonacci configuration? The approach used here is to convert the Fibonacci state to the corresponding Galois state, find the new Galois state as shown above, then convert the new Galois state back into Fibonacci form.

 Converting a Fibonacci state to the corresponding Galois state

 To convert a Fibonacci state into the corresponding Galois state, the equations for the Galois state must be written in terms of the current Fibonacci state, f0 (t) through f6(t).
The current Fibonacci state holds future register zero states:
f0 (t) = f0 (t+0)
f1 (t) = f0 (t+1)
f2 (t) = f0 (t+2)
f3 (t) = f0 (t+3)
f4 (t) = f0 (t+4)
f5 (t) = f0 (t+5)
f6 (t) = f0 (t+6)

Start with equations (4) and write the Galois state in terms of future register zero states
g0 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1)
g1 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4)
g2 (t) = g0 (t-2) ^ g0 (t-1)
g3 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-2) ^ g0 (t-1)
g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)
g6 (t) = g0 (t-7) ^ g0 (t-5) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)

Equations used to shift t-7 through t-1 references to t+0 through t+6:
0 = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1) ^ g0 (t+0)
0 = g0 (t-6) ^ g0 (t-5) ^ g0 (t-3) ^ g0 (t+0) ^ g0 (t+1)
0 = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2) ^ g0 (t+1) ^ g0 (t+2)
0 = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1) ^ g0 (t+2) ^ g0 (t+3)
0 = g0 (t-3) ^ g0 (t-2) ^ g0 (t+0) ^ g0 (t+3) ^ g0 (t+4)
0 = g0 (t-2) ^ g0 (t-1) ^ g0 (t+1) ^ g0 (t+4) ^ g0 (t+5)
0 = g0 (t-1) ^ g0 (t+0) ^ g0 (t+2) ^ g0 (t+5) ^ g0 (t+6)

g1 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4)
       = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1) ^ g0 (t+0)
       = g0 (t-1) ^ g0 (t+0)
       = g0 (t-1) ^ g0 (t+0) ^ g0 (t-1) ^ g0 (t+0) ^ g0 (t+2) ^ g0 (t+5) ^ g0 (t+6)
       = g0 (t+2) ^ g0 (t+5) ^ g0 (t+6)

g2 (t) = g0 (t-2) ^ g0 (t-1)
       = g0 (t-2) ^ g0 (t-1)
       = g0 (t-2) ^ g0 (t-1) ^ g0 (t-2) ^ g0 (t-1) ^ g0 (t+1) ^ g0 (t+4) ^ g0 (t+5)
       = g0 (t+1) ^ g0 (t+4) ^ g0 (t+5)

g3 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-2) ^ g0 (t-1)
       = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-2) ^ g0 (t-1) ^ g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1) ^ g0 (t+0)
       = g0 (t-3) ^ g0 (t-2)^ g0 (t+0)
       = g0 (t-3) ^ g0 (t-2)^ g0 (t+0) ^ g0 (t-3) ^ g0 (t-2) ^ g0 (t+0) ^ g0 (t+3) ^ g0 (t+4)
       = g0 (t+3) ^ g0 (t+4)

g4 (t) = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
       = g0 (t-4) ^ g0 (t-3) ^ g0 (t-1) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-1) ^ g0 (t+2) ^ g0 (t+3)
       = g0 (t+2) ^ g0 (t+3)

g5 (t) = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2)
       = g0 (t-5) ^ g0 (t-4) ^ g0 (t-2) ^ g0 (t-5) ^ g0 (t-4) ^ g0 (t-2) ^ g0 (t+1) ^ g0 (t+2)
       = g0 (t+1) ^ g0 (t+2)

g6 (t) = g0 (t-7) ^ g0 (t-5) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-1)
       = g0 (t-7) ^ g0 (t-5) ^ g0 (t-4) ^ g0 (t-3) ^ g0 (t-1) ^ g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1) ^ g0 (t+0)
       = g0 (t-5) ^ g0 (t-3) ^ g0 (t-6) ^ g0 (t+0)
       = g0 (t-5) ^ g0 (t-3) ^ g0 (t-6) ^ g0 (t+0) ^ g0 (t-6) ^ g0 (t-5) ^ g0 (t-3) ^ g0 (t+0) ^ g0 (t+1)
       = g0 (t+1)

g0 (t) = g0 (t)
g1 (t) = g0 (t+2) ^ g0 (t+5) ^ g0 (t+6)
g2 (t) = g0 (t+1) ^ g0 (t+4) ^ g0 (t+5)
g3 (t) = g0 (t+3) ^ g0 (t+4)
g4 (t) = g0 (t+2) ^ g0 (t+3)
g5 (t) = g0 (t+1) ^ g0 (t+2)
g6 (t) = g0 (t+1)

g0 (t) = f0 (t)
g1 (t) = f0 (t+2) ^ f0 (t+5) ^ f0 (t+6)
g2 (t) = f0 (t+1) ^ f0 (t+4) ^ f0 (t+5)
g3 (t) = f0 (t+3) ^ f0 (t+4)
g4 (t) = f0 (t+2) ^ f0 (t+3)
g5 (t) = f0 (t+1) ^ f0 (t+2)
g6 (t) = f0 (t+1)

 g0 (t) = f0 (t)                    (5)
 g1 (t) = f2 (t) ^ f5 (t) ^ f6 (t) 
 g2 (t) = f1 (t) ^ f4 (t) ^ f5 (t) 
 g3 (t) = f3 (t) ^ f4 (t)          
 g4 (t) = f2 (t) ^ f3 (t)          
 g5 (t) = f1 (t) ^ f2 (t)          
 g6 (t) = f1 (t)                   
The coefficients for the terms in the above equations can also be found with a calculation involving the polynomial and coefficients from equations (4):
    f0···f6                   p0····p7 t-7·t-1
g0  1000000    gf2util modmul,11010011,1101001,10000000
g1  0010011    gf2util modmul,11010011,1101000,10000000
g2  0100110    gf2util modmul,11010011,0000011,10000000
g3  0001100    gf2util modmul,11010011,1101111,10000000
g4  0011000    gf2util modmul,11010011,0001101,10000000
g5  0110000    gf2util modmul,11010011,0011010,10000000
g6  0100000    gf2util modmul,11010011,1011101,10000000
Converting a Galois state to the corresponding Fibonacci state

 To convert a Galois state into the corresponding Fibonacci state, stare with equations (5) and solve for f0 (t) - f6 (t) in terms of g0 (t) - g6 (t):
g0 (t) = f0 (t)
g1 (t) = f2 (t) ^ f5 (t) ^ f6 (t) 
g2 (t) = f1 (t) ^ f4 (t) ^ f5 (t) 
g3 (t) = f3 (t) ^ f4 (t) 
g4 (t) = f2 (t) ^ f3 (t) 
g5 (t) = f1 (t) ^ f2 (t) 
g6 (t) = f1 (t)
f0 (t) = g0 (t)
f1 (t) = g6 (t)
f2 (t) = g5 (t) ^ f1 (t)
       = g5 (t) ^ g6 (t)
f3 (t) = g4 (t) ^ f2 (t)
       = g4 (t) ^ g5 (t) ^ g6 (t)
f4 (t) = g3 (t) ^ f3 (t)
       = g3 (t) ^ g4 (t) ^ g5 (t) ^ g6 (t)
f5 (t) = g2 (t) ^ f1 (t) ^ f4 (t)
       = g2 (t) ^ g3 (t) ^ g4 (t) ^ g5 (t)
f6 (t) = g1 (t) ^ f2 (t) ^ f5 (t)
       = g1 (t) ^ g2 (t) ^ g3 (t) ^ g4 (t) ^ g6 (t)

 f0 (t) = g0 (t)                                      (6)
 f1 (t) = g6 (t)                                     
 f2 (t) = g5 (t) ^ g6 (t)                            
 f3 (t) = g4 (t) ^ g5 (t) ^ g6 (t)                   
 f4 (t) = g3 (t) ^ g4 (t) ^ g5 (t) ^ g6 (t)          
 f5 (t) = g2 (t) ^ g3 (t) ^ g4 (t) ^ g5 (t)          
 f6 (t) = g1 (t) ^ g2 (t) ^ g3 (t) ^ g4 (t) ^ g6 (t) 

The coefficients for the terms in the above equations can also be found with a calculation involving the polynomial:

    g0···g6
f0  1000000                            p7···p1
f1  0000001     gf2util divide,1000000,1100101
f2  0000011     gf2util divide,10000000,1100101
f3  0000111     gf2util divide,100000000,1100101
f4  0001111     gf2util divide,1000000000,1100101
f5  0011110     gf2util divide,10000000000,1100101
f6  0111101     gf2util divide,100000000000,1100101

Finding the time delay between LFSR stages

It can be seen from inspection of the circuit that the output of each Fibonacci stage differs from the output of a neighboring stage by one clock. But for the Galois configuration, the relationship is not as simple. A brute force approach for finding the delay for a register in the Galois configuration is to solve for each possible delay until one is found that is in the form of a single g0 term. For example, find g1 (t) as a function of the g0 output delayed by some number of clocks. 

g0 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4) ^ g0 (t-1)   ;from equations (4)
g1 (t) = g0 (t-7) ^ g0 (t-6) ^ g0 (t-4)
                                                          t-1····t-9
0 = g0 (t-0) ^ g0 (t-1) ^ g0 (t-4) ^ g0 (t-6) ^ g0 (t-7)  11001011
0 = g0 (t-1) ^ g0 (t-2) ^ g0 (t-5) ^ g0 (t-7) ^ g0 (t-8)   11001011
0 = g0 (t-2) ^ g0 (t-3) ^ g0 (t-6) ^ g0 (t-8) ^ g0 (t-9)    11001011

 t-1··················································································t-89
 0001011         g1 (t) = g0 (t-4) ^ g0 (t-6) ^ g0 (t-7)                                 ·
    11001011     0      = g0 (t-4) ^ g0 (t-5) ^ g0 (t-8) ^ g0 (t-10) ^ g0 (t-11)         ·
     1111011     g1 (t) = g0 (t-5) ^ g0 (t-6) ^ g0 (t-7) ^ g0 (t-8 ) ^ g0 (t-10) ^  g0 (t-11)
     11001011    0      = g0 (t-5) ^ g0 (t-6) ^ g0 (t-9) ^ g0 (t-11) ^ g0 (t-12)         ·
       111101                                                                            ·
       11001011                                                                          ·
         111111                                                                          ·
         11001011                                                                        ·
           110111                                                                        ·
           11001011                                                                      ·
              10111                                                                      ·
              11001011                                                                   ·
               1110011                                                                   ·
               11001011                                                                  ·
                 101101                                                                  ·
                 11001011                                                                ·
                  1111111                                                                ·
                  11001011                                                               ·
                    110101                                                               ·
                    11001011                                                             ·
                       11111                                                             ·
                       11001011                                                          ·
                         110011                                                          ·
                         11001011                                                        ·
                              111                                                        ·
                              11001011                                                   ·
                                101011                                                   ·
                                11001011                                                 ·
                                 1100111                                                 ·
                                 11001011                                                ·
                                      101                                                ·
                                      11001011                                           ·
                                       1101011                                           ·
                                       11001011                                          ·
                                          11101                                          ·
                                          11001011                                       ·
                                            100011                                       ·
                                            11001011                                     ·
                                             1000111                                     ·
                                             11001011                                    ·
                                              1000101                                    ·
                                              11001011                                   ·
                                               1000001                                   ·
                                               11001011                                  ·
                                                1001001                                  ·
                                                11001011                                 ·
                                                 1011001                                 ·
                                                 11001011                                ·
                                                  1111001                                ·
                                                  11001011                               ·
                                                    111001                               ·
                                                    11001011                             ·
                                                      101111                             ·
                                                      11001011                           ·
                                                       1110111                           ·
                                                       11001011                          ·
                                                         100101                          ·
                                                         11001011                        ·
                                                          1011111                        ·
                                                          11001011                       ·
                                                           1110101                       ·
                                                           11001011                      ·
                                                             100001                      ·
                                                             11001011                    ·
                                                              1001111                    ·
                                                              11001011                   ·
                                                               1010101                   ·
                                                               11001011                  ·
                                                                1100001                  ·
                                                                11001011                 ·
                                                                    1001                 ·
                                                                    11001011             ·
                                                                     1011011             ·
                                                                     11001011            ·
                                                                      1111101            ·
                                                                      11001011           ·
                                                                        110001           ·
                                                                        11001011         ·
                                                                            1111         ·
                                                                            11001011     ·
                                                                              111011     ·
                                                                              11001011   ·
                                                                                100111   ·
                                                                                11001011 ·
                                                                                 1010111 ·
                                                                                 11001011·
                                                                                  1100101·
                                                                                  11001011
                        g1 (t) = g0 (t-89)                                               1

This shows that the g1 output is the same as the g0 output 89 clocks ago. The delays for the other outputs can be found by the same method (or by inspection if no gate feeds the stage):

g1 (t) = g0 (t-89)
g2 (t) = g0 (t-90)
g3 (t) = g0 (t-85)
g4 (t) = g0 (t-86)
g5 (t) = g0 (t-87)
g6 (t) = g0 (t-127)
No doubt there is a more efficient way of finding these delay values!
More examples

Here is an example using a primitive trinomial.