example 1
Software such as REW, Audacity, SOX and others can generate a steady sine wave test tone and write it to a PCM encoded wav file. How far from ideal is the reconstructed result? Differences between an ideal sine wave and a perfectly reconstructed PCM file are due to encoding round-off losses, and in some cases to imperfections in the encoding software. Unwanted noise harmonics due to encoding round-off loss can be minimized but not eliminated by increasing sample bit depth. Unwanted noise harmonics due to encoding round-off loss can be completely eliminated by using a sample rate of 3, 4, or 6 times the sine frequency.
Part I: PCM encoded sine wave imperfections due to encoding round-off losses (quantization error)
Here are 3 example sine test tone wav files along with their spectrums in graphical and tabular form. The examples use 16 bit integer samples to encode sine at maximum amplitude. If 24 bit samples are used, the quantization noise peaks are reduced by roughly 48 dB, while the fundamental remains at at -3.01 dB (where 0 dB corresponds to a maximum amplitude square wave). With 16-bit samples, the noise peaks are at least 94.5 dB below fundamental peak, with an exact magnitude that is a function of the encoding round-off loss for each sample. No dithering is used in these examples. For a digitized sine wave, the need for and effect of dithering depends on the sample rate, sine frequency, and sample bit depth. For the 3 special cases of sample rate 3X, 4X, or 6X the sine frequency, dithering is actually harmful because there are no noise harmonics at all. Once the spectrum of the undithered result is known, it's easy to decide if dithering is appropriate.
Viewing the spectrum of an undithered PCM sine wave shows that the desired frequency is often accompanied by small amounts of unwanted noise harmonics. The harmonics are integer multiples of
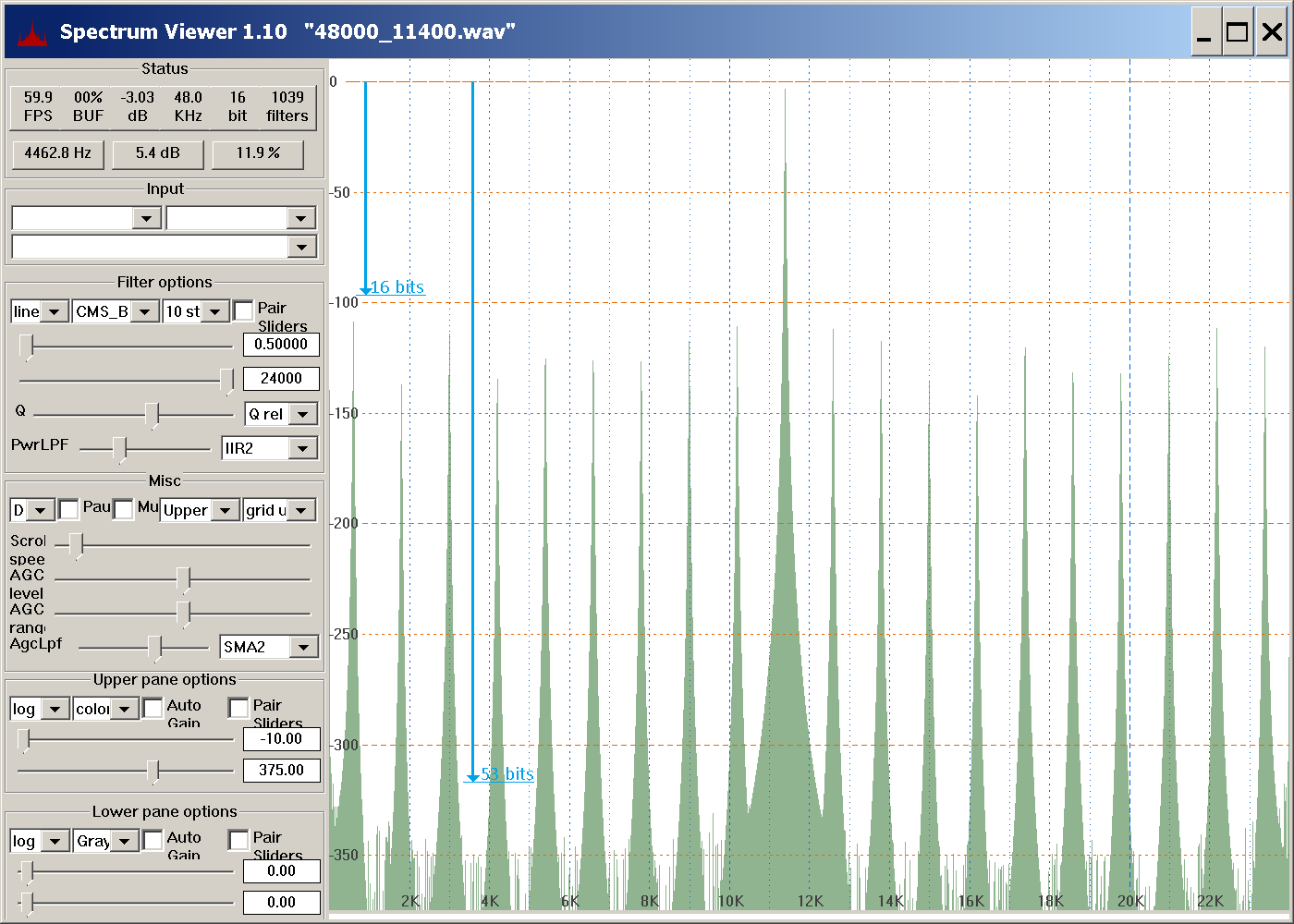
Here is example 1. There are 20 equally spaced harmonics:

example 1
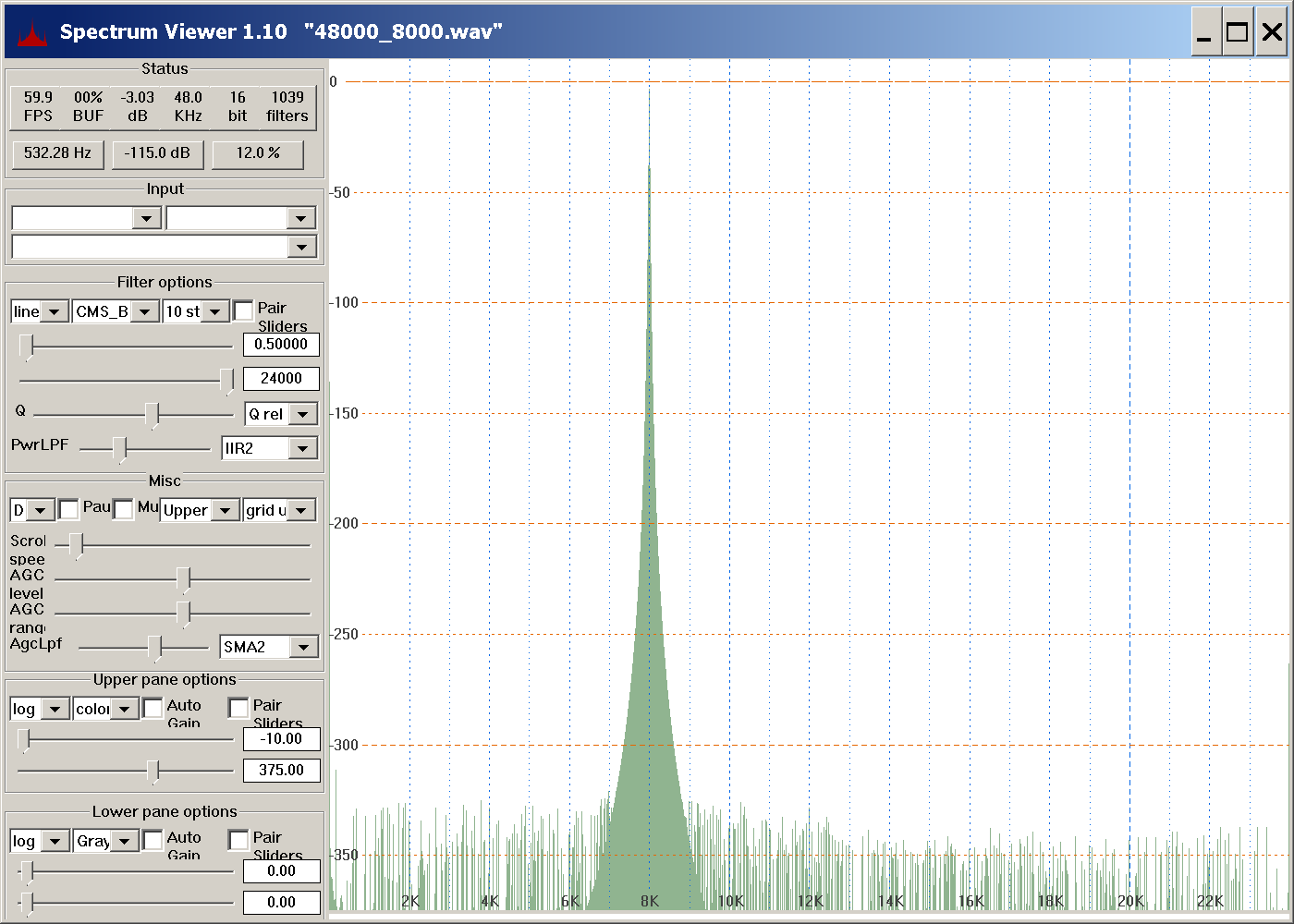
In 3 special cases (sample rate 3X, 4X, or 6X sine frequency), there are no unwanted harmonics at all. Here is a 6X example:
The noise peaks below 300 dB are due to the spectrum viewer software itself, and are not part of the input. The first example, a 11400 Hz sine wave sampled 48000 times per second, shows the fundamental along with 19 noise harmonics, for a total of 20 harmonics. Because 16-bit integer samples are used and the amplitude is maximimum, the noise harmonics are 96 dB or more below the fundamental harmonic.
In the second example, the sine frequency is changed to 8000 Hz. With this 6:1 sample rate to sine frequency ratio, there are no round-off induced noise harmonics at all.
For a third example, consider the same as above but with sine frequency 997 Hz:
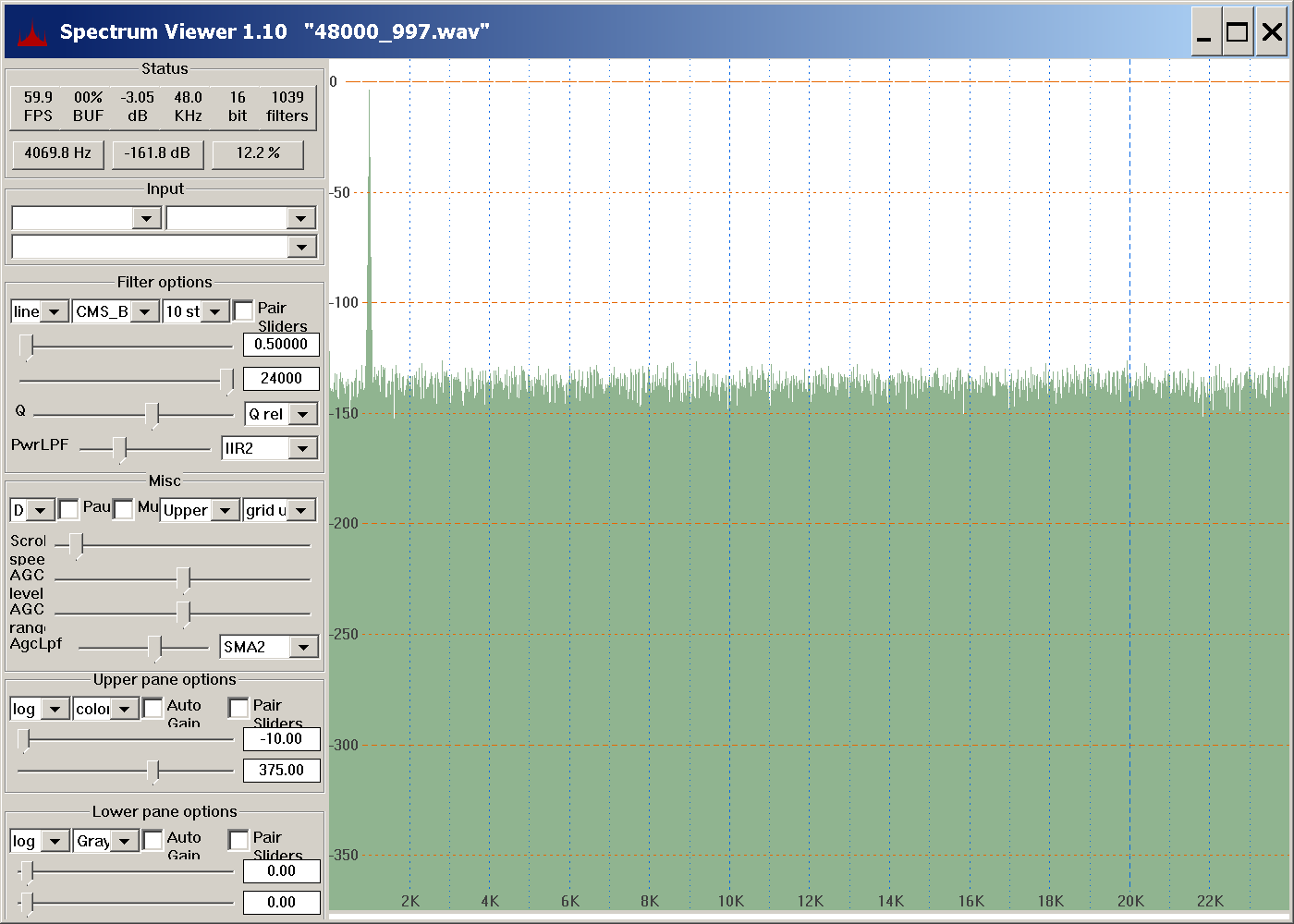
For sine frequency 997 Hz above, there are too many noise harmonics to count without zooming in on a smaller frequency range. Here is a view zoomed to a 20 Hz range:
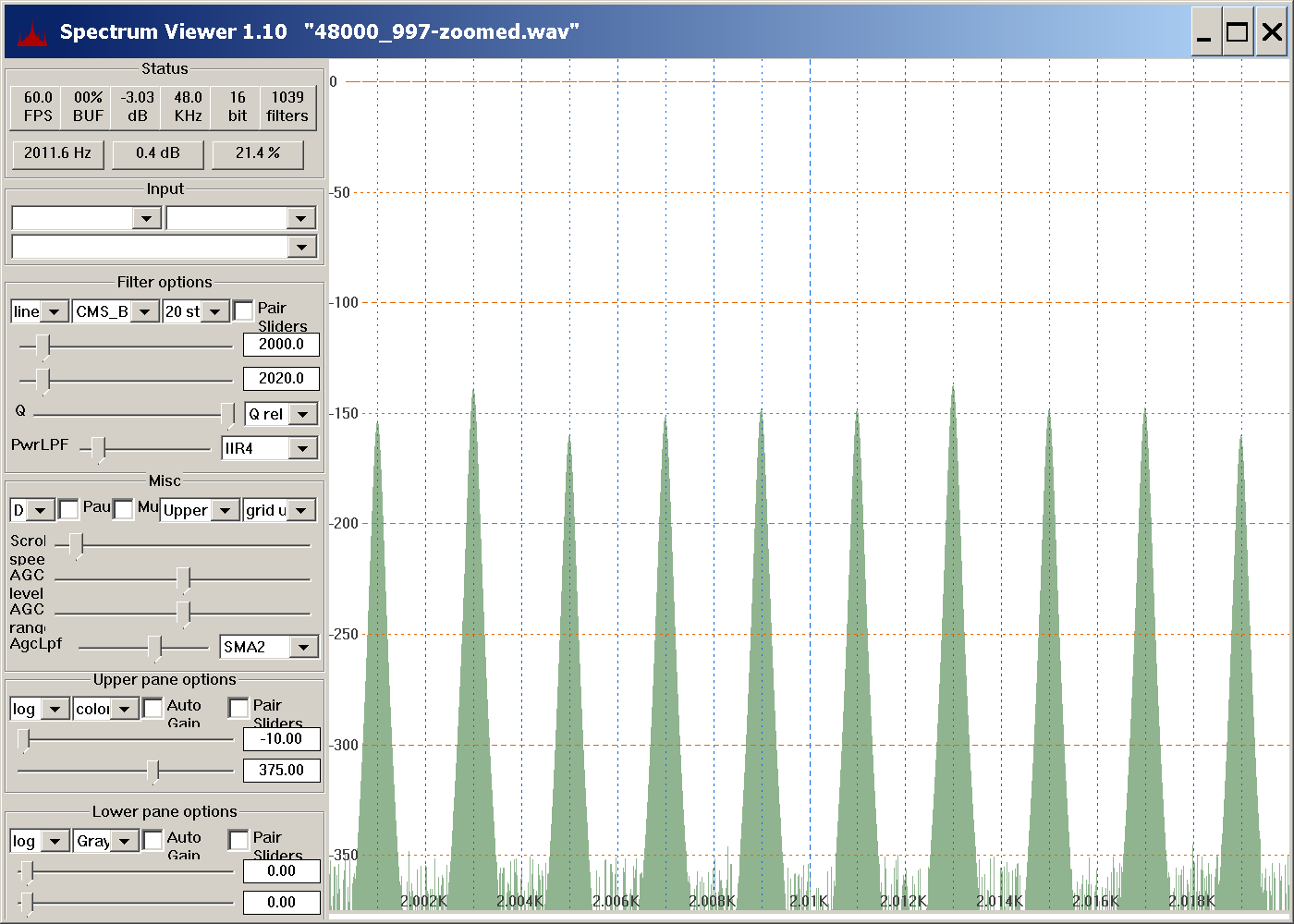
The zoomed view shows peaks at 2001, 2003, 2005, ..., 2019. Zooming to other ranges confirms peaks at every odd integer from 1 to 23999, for a total of 12,000 harmonics.
How can we calculate the number and positions of the peaks? It's actually easy. The generated samples will start repeating at some point. The number of samples in the repeating pattern is called N, and can be as little as 3. The repeating pattern will contain one or more complete cycles of the output sine wave fundamental frequency. Because of round-off error, smaller harmonics at integer multiples of the fundamental will be present. Calculate N by reducing the fraction formed from sample rate / sine frequency. The resulting numerator is N and the denominator is the number of sine cycles in the pattern. Here are some examples:
Sample Sine
Samples Sine Harmonics
Pattern Pattern
Rate Frequency
Per Pattern Cycles
Period Frequency
(Hz) (Hz)
(N)
(seconds) (Hz)
48000
11400 80
19 20
0.001667 600
48000 8000
6 1
1
0.000125 8000
48000 997
48000 997
12000 1.0
1
48000 1000.001
48000000 1000001 12000000
1000.0 0.001
Because the sample sequence repeats after N samples, we know it's periodic and therefore can be represented by a Fourier series of sine waves having frequencies that are integer multiples of the pattern fundamental frequency (Sample rate / N). A bigger list of N:cycles:harmonics is here.
The total number of harmonics, as shown in column 5 of the table above, can be computed as follows:
// one symmetry always present
because sine (a) = -sine (a+pi)
int harmonics = samplesPerPattern / 2;
// additional symmetry when cycles odd and samples even: sine (a) = sine (pi -
a)
if (cyclesPerPattern % 2 && samplesPerPattern % 2 == 0) harmonics /= 2;
The magnitude of the harmonics can be found by using a Discrete Fourier transform on the N sample values forming the repeating pattern. Here are the Discrete Fourier transforms for the 4 examples above. 2048 bit precision MPFR floating point is used for both sine and DFT calculations:
Example 1:
spectrumViewer generate out.wav i16 48000 0 sine:2048
1.0 11400 & spectrumViewer dft:2048.2 out.wav
Harmonic Frequency Level angle
(Hz) (dB) (deg)
1 600 -108.39 -90.00
3 1800 -135.40 -90.00
5 3000 -110.25 90.00
7 4200 -127.58 -90.00
9 5400 -114.62 90.00
11 6600 -116.76 90.00
13 7800 -120.55 -90.00
15 9000 -114.40 -90.00
17 10200 -109.43 -90.00
19 11400 -3.01 -90.00
21 12600 -111.86 90.00
23 13800 -115.86 -90.00
25 15000 -131.93 90.00
27 16200 -135.27 90.00
29 17400 -109.96 90.00
31 18600 -121.68 90.00
33 19800 -125.62 -90.00
35 21000 -120.77 90.00
37 22200 -110.42 -90.00
39 23400 -119.55 90.00
Example 2:
spectrumViewer generate out.wav i16 48000 0
sine:2048 1.0 8000 & spectrumViewer dft:2048.2 out.wav
Harmonic Frequency Level angle
(Hz) (dB) (deg)
1 8000 -3.01 -90.00
Example 3 (this one is long, so use double precision FFT
for speed):
spectrumViewer generate out.wav i16 48000 0
sine:2048 1.0 997 & spectrumViewer fft out.wav
Harmonic Frequency Level angle
(Hz) (dB) (deg)
1 1 -156.79 -90
3 3 -143.46 -90
5 5 -147.52 90
. . .
993 993 -145.42 90
995 995 -141.05 90
997 997 -3.01 -90
999 999 -156.61 -90
1001 1001 -141.95 90
. . .
23995 23995 -138.31 -90
23997 23997 -151.22 90
23999 23999 -140.68 -90
Worse case 16-bit harmonic noise
Here is the worse case noise for a 1000 Hz 16-bit PCM sine wave I could find using a quick search:
spectrumViewer generate out.wav i16 5000 0 sine:5120 0.99644553 1000 & spectrumViewer dft:5120.8 out.wav
Harmonic Frequency Level angle
(Hz) (dB) (deg)
1 1000 -3.04126739 -90.00000000
2 2000 -97.53863305 90.00000000
In the above example, a 5X sample rate to sine frequency ratio is used. This choice results in a single noise harmonic to maximize. The search program scans through many amplitude values looking for the worse case combination of rounding between the two samples corresponding to the two harmonics. The amplitude remains close to 1.0 so that it doesn't affect the result directly. In this example, the fundamental is only 94.497 dB above the noise harmonic.